Matriks dapat digunakan untuk mempermudah dalam menentukan penyelesaian sistem persamaan linear. Pada pembahasan kali ini, kita akan menggunakannya untuk menyelesaikan sistem persamaan linear dua variabel dan tiga variabel.
1. Sistem Persamaan Linear Dua Variabel
Bentuk umum sistem persamaan linear dua variabel adalah
ax + by = p ............................................................................ (1)
cx + dy = q ............................................................................. (2)
Persamaan (1) dan (2) di atas dapat kita susun ke dalam bentuk matriks seperti di bawah ini.
Tujuan penyelesaian sistem persamaan linear dua variabel adalah menentukan nilai x dan y yang memenuhi sistem persamaan itu. Oleh karena itu, berdasarkan penyelesaian matriks bentuk AX = B dapat dirumuskan sebagai berikut.
asalkan ad – bc ≠ 0.
Contoh Soal 23 :
Tentukan penyelesaian dari sistem persamaan linear berikut dengan cara matriks.
2x + y = 7
x + 3y = 7
Jawab:
Dari persamaan di atas dapat kita susun menjadi bentuk matriks sebagai berikut.
Dengan menggunakan rumus penjelasan persamaan matriks di atas, diperoleh sebagai berikut.
Jadi, diperoleh penyelesaian x = 1 dan y = 2.
2. Sistem Persamaan Linear Tiga Variabel
Kalian tentu tahu bahwa untuk menyelesaikan sistem persamaan linear tiga variabel dapat dilakukan dengan beberapa cara, misalnya eliminasi, substitusi, gabungan antara eliminasi dan substitusi, operasi baris elementer, serta menggunakan invers matriks. Kalian dapat menggunakan cara-cara tersebut dengan bebas yang menurut kalian paling efisien dan paling mudah.
Misalkan diberikan sistem persamaan linear tiga variabel berikut.
a1x + b1y + c1z = d1
a2x + b2y + c2z = d2
a3x + b3y + c3z = d3Sistem persamaan linear di atas dapat kita susun ke dalam bentuk matriks seperti berikut.
Misalkan A =
Bentuk di atas dapat kita tuliskan sebagai AX = B.
Penyelesaian sistem persamaan AX = B adalah X = A-1 B. Dalam hal ini, A-1 =
Oleh karena itu, diperoleh :
asalkan det A ≠ 0.
Contoh Soal 24 :
Tentukan himpunan penyelesaian dari sistem persamaan berikut.
2x + y – z = 1
x + y + z = 6
x – 2y + z = 0
Jawaban :
Cara 1:
Operasi elemen baris, selain dapat digunakan untuk mencari invers matriks, dapat pula digunakan untuk menyelesaikan sistem persamaan linear.
Dengan menggunakan operasi baris elementer.
Dengan demikian, diperoleh y = 2. Kita substitusikan nilai y = 2 ke persamaan (2) sehingga :
y + 3z = 11 ↔ 2 + 3z = 11
↔ 3z = 11 – 2
↔ 3z = 9
↔ z = 3
Substitusikan y = 2 dan z = 3 ke persamaan (1) sehingga diperoleh :
x + y + z = 6 ↔ x + 2 + 3 = 6
↔ x + 5 = 6
↔ x = 6 – 5
↔ x = 1
Jadi, penyelesaiannya adalah x = 1, y = 2, dan z = 3.
Dengan demikian, himpunan penyelesaiannya adalah {(1, 2, 3)}.
Cara 2:
Sistem persamaan linear di atas dapat kita susun ke dalam bentuk matriks sebagai berikut.
Misalkan A =
Dengan menggunakan minor-kofaktor, diperoleh :
det A =
det A = 2(3) – 1(0) + (–1)(–3) = 9
Dengan menggunakan minor-kofaktor, diperoleh :
Dengan cara yang sama, kalian akan memperoleh K31 = 2, K32 = –3, dan K33 = 1 (coba tunjukkan).
Dengan demikian, diperoleh :
kof(A) =
Oleh karena itu, adj(A) = (kof(A))T.
Adj(A) =
Jadi, X =
Jadi, diperoleh x = 1, y = 2, dan z = 3. Dengan demikian, himpunan penyelesaian sistem persamaan di atas adalah {(1, 2, 3)}.
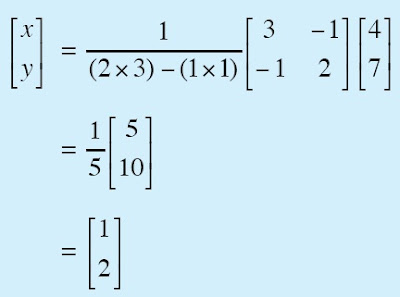
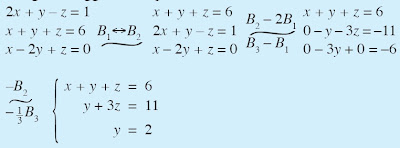

gambarnya mana......
BalasHapusKomentar ini telah dihapus oleh pengarang.
Hapusgambar apa hat
Hapusyusuf degil nian
BalasHapusapa nanda
BalasHapusKomentar ini telah dihapus oleh pengarang.
BalasHapusbentilah oey, marah yang punyo blog gek
BalasHapusapa rifqi
BalasHapusbelajar lah ndol
BalasHapusoi udah lah jok dak enak dgn apk dwi
BalasHapussudah
BalasHapusangka diatas tu hat, bukan gambar
BalasHapusiyo hat
BalasHapusbiji kau hat
BalasHapusKomentar ini telah dihapus oleh pengarang.
BalasHapusKomentar ini telah dihapus oleh pengarang.
BalasHapusKomentar ini telah dihapus oleh pengarang.
BalasHapus(y)
Hapussudah lah yok belajar lagi dak enak dg pak dwi
BalasHapuswoi tengok aspihani
BalasHapusjadi lah oi.. jangan rusuh blog orang -_-
BalasHapusmandi up
BalasHapusKomentar ini telah dihapus oleh pengarang.
BalasHapusKomentar ini telah dihapus oleh pengarang.
BalasHapusyang sistem 2 variabel yang contoh soal, di soalnya 2x + y = 7 kenapa pas dijadikan sistem matriks jadi 4
BalasHapusyang cara dua itu kok bisa hasilnya x,y,z= 1,2,3... jelasin dong.. uda lupa nihh ...
BalasHapusKurang paham soal matriks yang 2 variabel, dapat 4,7 dari mana ya??
BalasHapusyang pas cara ke 2.. cara ubah ke non kofaktor nya gimana?
BalasHapusyang pas cara ke 2.. cara ubah ke non kofaktor nya gimana?
BalasHapusRekomendasi artikel terkait -< Penyelesaian Sistem Persamaan Linear
BalasHapus1,2,-3 loh jawabannya.
BalasHapus(-3+30)×1/9= -3
HapusKomentar ini telah dihapus oleh pengarang.
BalasHapusyang 4 variabel itu gimina cara pengerjaannya ?
BalasHapusKomentar ini telah dihapus oleh pengarang.
BalasHapusMin, kalau 10 persamaan linear dan 4 variabel, bagaimana cara penyelesaiannya?
BalasHapus5
BalasHapus10
Itu darimana??
min kalo boleh saran jangan naro iklan di tengah artikel
BalasHapusMakasi min
BalasHapusMakasi min
BalasHapusBelum paham
BalasHapuslol
BalasHapusLel
BalasHapusterima kasih!
BalasHapusCara mengubah ke faktornya
BalasHapusTolong jawap dong soalnya
BalasHapus