Matriks Penjumlahan dan Pengurangan

Matriks : 

Dalam matematika, matriks adalah kumpulan bilangan, simbol, atau ekspresi, berbentuk persegi panjang yang disusun menurut baris dan kolom. Bilangan-bilangan yang terdapat di suatu matriks disebut dengan elemen atau anggota matriks. Contoh matriks dengan 2 baris dan 3 kolom yaitu

Pemanfaatan matriks misalnya dalam menemukan solusi sistem persamaan linear. Penerapan lainnya adalah dalam transformasi linear, yaitu bentuk umum dari fungsi linear, misalnya rotasi dalam 3 dimensi.

Matriks seperti halnya variabel biasa dapat dimanipulasi, seperti dikalikan, dijumlah, dikurangkan dan didekomposisikan. Dengan representasi matriks, perhitungan dapat dilakukan dengan lebih terstruktur.

contoh Matriks :

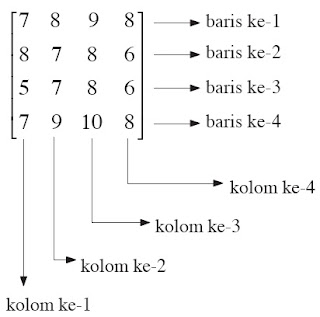
Matriks-Matriks Khusus

Beberapa macam matriks khusus yang perlu kalian kenal adalah sebagai berikut.

a. Matriks Baris

Matriks baris adalah matriks yang hanya terdiri atas satu baris.

Misalnya:

P = [3 2 1]

Q = [4 5 –2 5]

b. Matriks Kolom

Matriks kolom adalah matriks yang hanya terdiri atas satu kolom, Misalnya:

c. Matriks Persegi

Matriks persegi adalah matriks yang banyak baris sama dengan banyak kolom. Jika banyak baris matriks persegi A adalah n maka banyaknya kolom juga n, sehingga ordo matriks A adalah n × n. Seringkali matriks A yang berordo n × n disebut dengan matriks persegi ordo n. Elemen-elemen a₁₁, a₂₂, a₃₃, ..., a_nn merupakan elemen-elemen pada diagonal utama.

Misalnya:

A =  merupakan matriks persegi ordo 2.

B =  merupakan matriks persegi ordo 4.

Elemen-elemen diagonal utama matriks A adalah 1 dan 10, sedangkan pada matriks B adalah 4, 6, 13, dan 2.

d. Matriks Diagonal

Matriks diagonal adalah matriks persegi dengan setiap elemen yang bukan elemen-elemen diagonal utamanya adalah 0 (nol), sedangkan elemen pada diagonal utamanya tidak semuanya nol. Misalnya:

e. Matriks Identitas

Matriks identitas adalah matriks persegi dengan semua elemen pada diagonal utama adalah 1 (satu) dan elemen lainnya semuanya 0 (nol). Pada umumnya matriks identitas dinotasikan dengan I dan disertai dengan ordonya. Misalnya:

f. Matriks Nol

Matriks nol adalah suatu matriks yang semua elemennya adalah 0 (nol). Matriks nol biasanya dinotasikan dengan huruf O diikuti ordonya, O_{m × n}. Misalnya:

Notasi

Matriks pada umumnya ditulis dalam tanda kurung siku/kurung tegak:

A. Penjumlahan Dan Pengurangan Matriks

Dua buah matriks A dan B dapat dijumlah dan dikurang jika ordo keduanya sama hasil penjumlahan dan pengurangan matriks A dan B didapat dengan cara menjumlahkan atau mengurangkan unsur-unsur yang seletak.

Sifat-sifat penjumlahan dan pengurangan matriks :

(1) Pengurangan dua matriks merupakan penjumlahan dengan matriks lawannya.
      atau A – B = A + (–B)
(2) Misalkan A, B dan C adalah tiga matriks yang ordonya sama, maka berlaku :
     A + B = B + A
(3) Perkalian suatu bilangan real k dengan matriks A adalah suatu matriks kA yang didapat dengan cara          mengalikan setiap unsur matiriks A dengan k
     (A + B) + C = A + (B + C)
(4) Matriks nol adalah matriks yang semua elemennya adalah nol (dilambangkan dengan O). Matriks ini adalah matriks identitas penjumlahan, sehingga
      A + O = O + A = A (b) A + (–A) = O

Contoh Soal Penjumlahan dan penguragan Matriks :

1. Diketahui A =  , B =  , dan C =  Tentukan :

a. A + B;

b. A + C.

Penyelesaian :

a. A + B = 

b. A + C =   tidak dapat dijumlahkan karena ordonya tidak sama.

2. Diketahui A =  dan B =  . Tentukan A – B.

Jawaban :

Cara 1:

Karena –B =  maka

A – B = A + (–B) = 

Cara 2:

A – B = 

3. 

4. Diketahui persamaan matriks

Nilai a + b + c + d =

Pembahasan
Jumlahkan dua matriks pada ruas kiri, sementara kalikan dua matriks pada ruas kanan, terakhir gunakan kesamaan antara dua buah matriks untuk mendapatkan nilai yang diminta.



2 + a = −3
a = − 5

4 + b = 1
b = − 3

d − 1 = 4
d = 5

c − 3 = 3
c = 6

Sehingga

a + b + c + d = −5 − 3 + 6 + 5 = 3