INVERS MATRIKS:
Jika A dan B adalah matriks persegi, dan berlaku  maka dikatakan matriks A dan B saling invers. B disebut invers dari A, atau ditulis
maka dikatakan matriks A dan B saling invers. B disebut invers dari A, atau ditulis  . Matriks yang mempunyai invers disebut invertible atau matriks non singular, sedangkan matriks yang tidak mempunyai invers disebut matriks singular.
. Matriks yang mempunyai invers disebut invertible atau matriks non singular, sedangkan matriks yang tidak mempunyai invers disebut matriks singular.
Untuk mencari invers matriks persegi berordo 2×2, coba perhatikan berikut ini.
Jika dengan
dengan  , maka invers dari matriks A (ditulis
, maka invers dari matriks A (ditulis  ) adalah sebagai berikut:
) adalah sebagai berikut:
Jika
Jika  maka matriks tersebut tidak mempunyai invers, atau disebut matriks singular.
maka matriks tersebut tidak mempunyai invers, atau disebut matriks singular.
Sifat-sifat matriks persegi yang mempunyai invers:
Contoh: Diketahui A =  dan B =
dan B = 
Selidiki, apakah A dan B saling invers?
Penyelesaian :
Matriks A dan B saling invers jika berlaku A × B = B × A = I.
A × B = 
B × A = 
Karena A × B = B × A maka A dan B saling invers, dengan A–1 = B dan B–1 = A.
Menentukan Invers Matriks Berordo 2 × 2
Misalkan diketahui matriks A =  , dengan ad – bc ≠ 0.
, dengan ad – bc ≠ 0.
Suatu matriks lain, misalnya B dikatakan sebagai invers matriks A jika AB = I. Matriks invers dari A ditulis A–1 . Dengan demikian, berlaku :
AA–1 = A–1A = I
Matriks A mempunyai invers jika A adalah matriks nonsingular, yaitu det A ≠ 0. Sebaliknya, jika A matriks singular (det A = 0) maka matriks ini tidak memiliki invers.
Misalkan matriks A =  dan matriks B =
dan matriks B =  sehingga berlaku A × B = B × A = I. Kita akan mencari elemen-elemen matriks B, yaitu p, q, r, dan s.
sehingga berlaku A × B = B × A = I. Kita akan mencari elemen-elemen matriks B, yaitu p, q, r, dan s.
Dari persamaan A × B = I, diperoleh :
Jadi, diperoleh sistem persamaan :
ap + br = 1 dan aq + bs = 0
cp + dr = 0 cq + ds = 1
Dengan menyelesaikan sistem persamaan tersebut, kalian peroleh :
Dengan demikian,
Matriks B memenuhi A × B = I.
Sekarang, akan kita buktikan apakah matriks B × A = I?
Karena ad – bc ≠ 0, berlaku B × A =  = I
= I
Karena A × B = B × A = I maka B = A–1.
Jadi, jika A =
untuk ad – bc ≠ 0.
Contoh Soal 18 :
Tentukan invers matriks-matriks berikut.
Tentukan invers matriks-matriks berikut.
a. A =
b. B = 
Menentukan Invers Matriks Berordo 3 × 3 (Pengayaan)
Invers matriks berordo 3 × 3 dapat dicari dengan beberapa cara. Pada pembahasan kali ini kita akan menggunakan cara adjoin dan transformasi baris elementer.
a. Dengan Adjoin
Pada subbab sebelumnya, telah dijelaskan mengenai determinan matriks. Selanjutnya, adjoin A dinotasikan adj (A), yaitu transpose dari matriks yang elemen-elemennya merupakan kofaktor-kofaktor dari elemen-elemen matriks A, yaitu :
adj(A) = (kof(A))T
Adjoin A dirumuskan sebagai berikut.
Invers matriks persegi berordo 3 × 3 dirumuskan sebagai berikut.
Adapun bukti tentang rumus ini akan kalian pelajari lebih mendalam dijenjang pendidikan yang lebih tinggi.
Contoh Soal 19 :
Diketahui matriks A =  . Tentukan invers matriks A, misalnya kita gunakan perhitungan menurut baris pertama.
. Tentukan invers matriks A, misalnya kita gunakan perhitungan menurut baris pertama.
Jawaban :
Terlebih dahulu kita hitung determinan A.
det A = 
= 1(1) – 2(2) + 1(1) = –2
Dengan menggunakan rumus adjoin A, diperoleh :
adj(A) = 
Jadi, A–1 dapat dihitung sebagai berikut.
b. Dengan Transformasi Baris Elementer
Untuk menentukan invers matriks An dengan cara transformasi baris elementer, dapat dilakukan dengan langkah-langkah berikut berikut.
1) Bentuklah matriks (An | In), dengan In adalah matriks identitas ordo n.
2) Transformasikan matriks (An | In) ke bentuk (In | Bn), dengan transformasi elemen baris.
3) Hasil dari Langkah 2, diperoleh invers matriks An adalah Bn.
Notasi yang sering digunakan dalam transformasi baris elementer adalah :
a) Bi ↔ Bj : menukar elemen-elemen baris ke-i dengan elemen-elemen baris ke-j;
b) k.Bi : mengalikan elemen-elemen baris ke-i dengan skalar k;
c) Bi + kBj : jumlahkan elemen-elemen baris ke-i dengan k kali elemen-elemen baris ke-j.
Contoh Soal 20 :
Tentukan invers matriks A =  dengan transformasi baris elementer.
dengan transformasi baris elementer.
Penyelesaian :
Jadi, diperoleh A–1 = 
Keterangan :
1/2 B1 : Kalikan elemen-elemen baris ke-1 dengan 1/2.
B2 – 5B1 : Kurangkan baris ke-2 dengan 5 kali elemen-elemen baris ke-1.
B1 – B2 : Kurangi elemen-elemen baris ke-1 dengan elemen-elemen baris ke-2.
2B2 : Kalikan elemen-elemen baris ke-2 dengan 2.
Contoh Soal 21 :
Tentukan invers matriks A =  dengan transformasi baris elementer.
dengan transformasi baris elementer.
Jawaban :
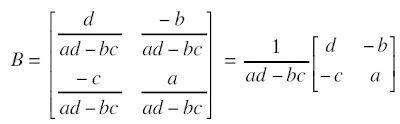

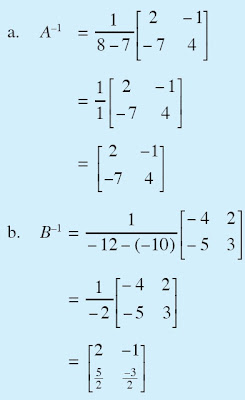




menarik sekali
BalasHapusApax yang menarikkkk
HapusYa apa webnya lah
HapusMenarik dimananya pusing mah iya
HapusKontol
HapusBikin puyeng lah pantek
HapusGblg
HapusMenarik sekali pergelutan ini
HapusAstagfirullahaladzim kamu ini berdosa banget
HapusPusing banget matematika ini, sudah muak akuu😭😭
HapusGimana caranya saya pintar matematika🤔
HapusBlajar👍
HapusNugudut sekk,, biar gk puyengg😂
HapusPuyeng Gan ������
BalasHapusWkwkwk
HapusSama slur
HapusBagus gan
BalasHapusSedikit bingung pake cara transformasi baris elementer tpi bagus gan :)
BalasHapusbro untuk lebih lengkap pembahasannya dan penjelasannya, mampir ke artikel ini aja Invers Matriks Matematika
BalasHapusPembodohan
Hapusnggak pembodohan si...cuma webnya udah mati aja om
HapusPuyeng gan
BalasHapussama moms
HapusBagus gan, sy jd ngerti👍
BalasHapuspaham
BalasHapuslumayan buat persiapan uts :D
BalasHapusKomentar ini telah dihapus oleh pengarang.
BalasHapuswokee
BalasHapuspusing kata"nya sharusnya di jelasin apa itu l gitu jadi ngerti belajar lagi ya gan bahasanya
BalasHapusaku pernah baca yang ada kalimatnya, cari aja di google... 6 langkah invers matriks 3x3 metode obe
Hapuskaya tae
BalasHapusBengek wkkw
HapusPuuuuciiiiiaaaang
BalasHapushatur nuhun gan. sangat membantu.
BalasHapuskalo boleh tau buku referensinya apa judulnya yah. mksh
Mantap
BalasHapusKeren.. Mampir jga..
BalasHapushttp://matematikakubisa.blogspot.com
Komentar ini telah dihapus oleh pengarang.
BalasHapusBanyak tipe matriks seperti matriks dengan orde 2x2, 3x3, 4x4 dan matriks dengan orde lainnya. Namun tidak semua matriks bisa diinvers, matriks yang tidak bisa di invers adalah matriks singular karena matriks singular akan menghasilkan determinan matriks menjadi nol. Selain itu untuk menghasilkan invers matriks dibutuhkan ketelitian dan pengetahuan anda mencari determinan matriks. matriks dengan orde 2x2 mudah di cari determinannya namun matriks dengan orde tinggi perlu metoda untuk mencari determinan matriks
BalasHapuswew, puyeng tp menarik
BalasHapuspada pencarian invers menggunakan baris elementer (matrik 3x3), itu b3-b1 atau b3-2b1
BalasHapusHadeh kok susah banget yq di mengerti..
BalasHapusHadeh kok susah banget yq di mengerti..
BalasHapusheheheh... memang susah susah gampang bikin artikel matematika... karena itu porosilmu.com sedikit artikel matematikanya.. good job bro... salam kenal..
BalasHapusSampe sekarang gua gak tau itu matriks penerapan dikehidupanny kyk gmna?. Yg tau jawab..
BalasHapusSecara logik, akan mampu berfikir dan bisa menyelesaikan masalah dan mencari jalan keluar dari keterpurukan,
Hapusatau akan bermanfaat bagi penganalisaan suatu sistem,
Sampe sekarang gua gak tau itu matriks penerapan dikehidupanny kyk gmna?. Yg tau jawab..
BalasHapuscontoh penggunaan dlm kehidupan : penyandian pesan rahasia
Hapussumber : buku bse matematika k13
Pikir aja sendiri😂😂😂😂😂😂😂
HapusNjir
BalasHapusSANGAT MEMBANTU...ARTICLE TERBAIK
BalasHapusrasanya sedih liatnya 😂😂 tapi membantu ╮(╯▽╰)╭
BalasHapusitu adjoin begimana dah yaallah
BalasHapusnumpang share gan,
BalasHapusblog pelajaran lengkap
https://pintarbelajar7.blogspot.co.id/
Aku kok bingung?
BalasHapusAku gh sama😂
HapusSangat membantu saya, terima kasih.
BalasHapusMy blog
Kenapa jawabannya ketutup sama gambarpower by codecogs?
BalasHapuspuyeng"
BalasHapusApakah matrix ordo 2x1 dapat diivers? Lalu, kalo bisa diivers, bagaimana pengerjaannya? Mohon penjelasannya.
BalasHapusInvers hanya berlaku pada matriks yang memiliki ordo yang sama
Hapusbagus tapi aga sulit di pahami untuk SMA
BalasHapusMsih sedikit bingung buat yng ordo 3x3 gan
BalasHapusTerimakasih...ijin copy ya..
BalasHapushttps://publicgoldindonesia.blogspot.com
Cukup baik
BalasHapusThanks,,,.saya mengerti
BalasHapusPuyeng
BalasHapusSusah paham kalau soal matematika😂
BalasHapusMati rasa gw cuk
BalasHapusterimaksih untuk informasinya.
BalasHapushttp://bit.ly/2TzNBmK
Bingung pembahasan materinya ...hmm
BalasHapus1-1 = -1 ? Hmmmmm
BalasHapusMalah promosi
BalasHapusMinta no WA donk min... Bantu aku please
BalasHapusCukup menarik penjelasannya. Tapi sayang saya tidak mengerti😭
BalasHapusPada ngerti?
BalasHapusKagak
HapusLo komentar bukan promosi jancok
BalasHapusSaya jadi sedikit paham tentang matriks
BalasHapusMati rasa gw gan :)
BalasHapusItu contoh soal no 18 gk ad jawabannya kah?
BalasHapusItu contoh soal no 18 gk ad jawabannya kah?
BalasHapusALLAHUAKBAR.
BalasHapusso ez
BalasHapusI Like Your Artcile. This Article is Amazing and Easy Tp Understand visit to know top Instagram Desigining account Click Here
BalasHapusBHAHHAHAHAKKK ngakakkk wkwkwk
BalasHapusNgertiin MTK ternyata lebih sulit dibanding ngertiin kamu yaa:")
BalasHapusanying curhat
Hapusawokwowkwokwowkwokwok goblok
BalasHapusgan,ko dibeber2in sihh rumus nya? :(
BalasHapusLOGIKA HARUS MAIN GUYS
BalasHapusJust admiring your work and wondering how you managed this blog so well. It’s so remarkable that I can't afford to not go through this valuable information whenever I surf the internet 검증사이트
BalasHapusSaya memiliki mimpi untuk bisa menguasai pelajaran seperti ini. Saya sangat mennyukainya. Jika mempunya mimpi yang ingin ditafsirkan silahkan lihat arti mimpi
BalasHapus