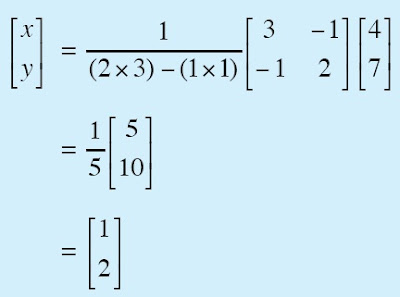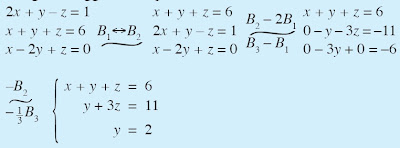Contoh dan Penyelesain Matrix

Menyelesaikan Sistem Persamaan Linear dengan Determinan

Menyelesaikan Sistem Persamaan Linear dengan Determinan :

Sistem persamaan linear yang disusun dalam bentuk matriks juga dapat ditentukan himpunan penyelesaiannya dengan metode determinan. Misalnya, sistem persamaan linear untuk dua variabel dan tiga variabel adalah sebagai berikut.

a. ax + by = p
cx + dy = q

b. a₁x + b₁y + c₁z = d₁

a₂x + b₂y + c₂z = d₂

a₃x + b₃y + c₃z = d₃
Pada sistem persaman linear dua variabel, bentuk tersebut dapat diubah ke bentuk matriks berikut.

This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.

This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.

, dengan A = This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.

, X =

, dan B =

.

D =

= ad – bc (Determinan koefisien x dan y, dengan elemen-elemen matriks A)

Dx = This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.

= pd – bq (Ganti kolom ke-1, dengan elemen-elemen matriks B)

Dy = This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.

= aq – cp (Ganti kolom ke-2, dengan elemen-elemen matriks B)

Nilai x dan y dapat ditentukan dengan rumus berikut.
This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.

Dengan cara yang sama dapat ditentukan D, D_x, D_y, dan D_z untuk sistem persamaan linear tiga variabel sebagai berikut.

Nilai x, y, dan z dapat ditentukan dengan cara berikut.

Contoh Soal 25 :

Tentukan penyelesaian sistem persamaan linear berikut dengan metode determinan.

a. 2x + y = 4
x – 2y = –3

b. x + y + z = 0
x + y – z = –2
x – y + z = 4

Penyelesaian :

a. Sistem persamaan linear di atas dapat disusun dalam bentuk matriks berikut.
This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.

Kita tentukan nilai D, D_x, D_y .
D = This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.

= – 4 – 1 = – 5
Dx = This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.

= – 8 – (–3) = – 5
Dy = This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.

= – 6 – 4 = – 10
Jadi, x = This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.

= 1 dan y = This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.

= 2.

b. Sistem persamaan linear tiga variabel di atas dapat disusun dalam bentuk matriks berikut.

Sistem persamaan linear tiga variabel matriks

Menyelesaikan Sistem Persamaan Linear dengan Invers Matriks

Menyelesaikan Sistem Persamaan Linear dengan Invers Matriks :

Sistem persamaan linier yang terdiri atas persamaan-persamaan (1), (2), dan (3) di atas dapat juga ditulis dengan bentuk notasi matriks AB = C seperti berikut

1	1	-1
8	3	-6
-4	-1	3

Solusinya adalah matriks B. Agar kita dapat mengisolasi B sendirian di salah satu sisi dari persamaan di atas, kita kalikan kedua sisi dari persamaan di atas dengan invers dari matriks A.

A⁻¹AB	=	A⁻¹C
B	=	A⁻¹C

Sekarang, untuk mencari B kita perlu mencari A⁻¹. Silakan melihat halaman tentang matriks untuk belajar bagaimana mencari invers dari sebuah matriks.

A⁻¹ =

-3	2	3
0	1	2
-4	3	5

B =

-3	2	3
0	1	2
-4	3	5

B =

Jadi solusinya adalah x = 2, y = 3, z = 4.

Metode ini dapat digunakan untuk menyelesaikan sistem persamaan linier dengan n variabel. Kalkulator di atas juga menggunakan metode ini untuk menyelesaikan sistem persamaan linier.

Eliminasi Gauss / Eliminasi Gauss-Jordan

Sistem persamaan liniear yang terdiri atas persamaan-persamaan(1), (2), dan (3) dapat juga dinyatakan dalam bentuk matriks teraugmentasi A seperti berikut

A =

1	1	-1	1
8	3	-6	1
-4	-1	3	1

Dengan melakukan serangkaian operasi baris (Eliminasi Gauss), kita dapat menyederhanakan matriks di atas untuk menjadi matriks Eselon-baris.

A =

1	0,375	-0,75	0,125
0	1	-0,4	1,4
0	0	1	4

Kemudian kita bisa substitusikan kembali nilai-nilai yang kita dapat untuk mencari nilai dari semua variabel. Atau, kita juga bisa meneruskan dengan serangkaian operasi baris lagi sehingga matriks di atas menjadi matriks yang Eselon-baris tereduksi (dengan menggunakan Eliminasi Gauss-Jordan).

A =

1	0	0	2
0	1	0	3
0	0	1	4

Dengan melakukan operasi Eliminasi Gauss-Jordan, kita mendapatkan solusi dari sistem persamaan linier di atas pada kolom terakhir: x = 2, y = 3, z = 4.

Penyelesaian Sistem Persamaan Linear dengan Matriks

PENYELESAIAN MATRIKS PERSAMAAN LINEAR 2 DAN 3 VARIABEL :
Matriks dapat digunakan untuk mempermudah dalam menentukan penyelesaian sistem persamaan linear. Pada pembahasan kali ini, kita akan menggunakannya untuk menyelesaikan sistem persamaan linear dua variabel dan tiga variabel.

1. Sistem Persamaan Linear Dua Variabel

Bentuk umum sistem persamaan linear dua variabel adalah

ax + by = p ............................................................................ (1)
cx + dy = q ............................................................................. (2)

Persamaan (1) dan (2) di atas dapat kita susun ke dalam bentuk matriks seperti di bawah ini.
This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.

Tujuan penyelesaian sistem persamaan linear dua variabel adalah menentukan nilai x dan y yang memenuhi sistem persamaan itu. Oleh karena itu, berdasarkan penyelesaian matriks bentuk AX = B dapat dirumuskan sebagai berikut.

This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.

asalkan ad – bc ≠ 0.

Contoh Soal 23 :

Tentukan penyelesaian dari sistem persamaan linear berikut dengan cara matriks.

2x + y = 7
x + 3y = 7

Jawab:

Dari persamaan di atas dapat kita susun menjadi bentuk matriks sebagai berikut.
This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.

Dengan menggunakan rumus penjelasan persamaan matriks di atas, diperoleh sebagai berikut.

Penyelesaian Sistem Persamaan Linear dengan Matriks

Jadi, diperoleh penyelesaian x = 1 dan y = 2.

2. Sistem Persamaan Linear Tiga Variabel

Kalian tentu tahu bahwa untuk menyelesaikan sistem persamaan linear tiga variabel dapat dilakukan dengan beberapa cara, misalnya eliminasi, substitusi, gabungan antara eliminasi dan substitusi, operasi baris elementer, serta menggunakan invers matriks. Kalian dapat menggunakan cara-cara tersebut dengan bebas yang menurut kalian paling efisien dan paling mudah.

Misalkan diberikan sistem persamaan linear tiga variabel berikut.

a₁x + b₁y + c₁z = d₁

a₂x + b₂y + c₂z = d₂

a₃x + b₃y + c₃z = d₃

Sistem persamaan linear di atas dapat kita susun ke dalam bentuk matriks seperti berikut.
This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.

Misalkan A = This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.

, X =

, dan B =

Bentuk di atas dapat kita tuliskan sebagai AX = B.
Penyelesaian sistem persamaan AX = B adalah X = A^-1 B. Dalam hal ini, A^-1 = This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.

Oleh karena itu, diperoleh :
This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.

asalkan det A ≠ 0.

Contoh Soal 24 :

Tentukan himpunan penyelesaian dari sistem persamaan berikut.

2x + y – z = 1
x + y + z = 6
x – 2y + z = 0

Jawaban :

Cara 1:

Operasi elemen baris, selain dapat digunakan untuk mencari invers matriks, dapat pula digunakan untuk menyelesaikan sistem persamaan linear.

Dengan menggunakan operasi baris elementer.

Dengan demikian, diperoleh y = 2. Kita substitusikan nilai y = 2 ke persamaan (2) sehingga :

y + 3z = 11 ↔ 2 + 3z = 11
↔ 3z = 11 – 2
↔ 3z = 9
↔ z = 3

Substitusikan y = 2 dan z = 3 ke persamaan (1) sehingga diperoleh :

x + y + z = 6 ↔ x + 2 + 3 = 6
↔ x + 5 = 6
↔ x = 6 – 5
↔ x = 1

Jadi, penyelesaiannya adalah x = 1, y = 2, dan z = 3.

Dengan demikian, himpunan penyelesaiannya adalah {(1, 2, 3)}.

Cara 2:

Sistem persamaan linear di atas dapat kita susun ke dalam bentuk matriks sebagai berikut.
Misalkan A = This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.

, X =

, dan B =

Dengan menggunakan minor-kofaktor, diperoleh :

det A = This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.

det A = 2(3) – 1(0) + (–1)(–3) = 9

Dengan menggunakan minor-kofaktor, diperoleh :

Dengan cara yang sama, kalian akan memperoleh K₃₁ = 2, K₃₂ = –3, dan K₃₃ = 1 (coba tunjukkan).

Dengan demikian, diperoleh :
kof(A) = This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.

Oleh karena itu, adj(A) = (kof(A))^T.
Adj(A) = This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.

Jadi, X =

Jadi, diperoleh x = 1, y = 2, dan z = 3. Dengan demikian, himpunan penyelesaian sistem persamaan di atas adalah {(1, 2, 3)}.

Penyelesaian Sistem Persamaan Linear dengan Matriks

PENYELESEAIN SISTEM PERSAMAAN LINEAR DENGAN MATRIKS :

Persamaan linear dapat dinyatakan sebagai matriks. Misalnya persamaan:

3x1 + 4x2 − 2 x3 = 5

x1 − 5x2 + 2x3 = 7

2x1 + x2 − 3x3 = 9

dapat dinyatakan dalam matriks teraugmentasisebagai berikut

$\begin{bmatrix} 3 & 4 & -2 & 5\\ 1 & -5 & 2 & 7\\ 2 & 1 & -3 & 9\\ \end{bmatrix}” /> <p style=$

Penyelesaian persamaan linier dalam bentuk matriks dapat dilakukan melalui beberapa cara, yaitu dengan eliminasi Gauss atau dapat juga dengan cara eliminasi Gauss-Jordan. Namun, suatu sistem persamaan linier dapat diselesaikan dengan eliminasi Gauss untuk mengubah bentuk matriks teraugmentasi ke dalam bentuk eselon-baris tanpa menyederhanakannya. Cara ini disebut dengan substitusi balik.

Sebuah sisitem persamaan linier dapat dikatakan homogen apabila mempunyai bentuk :

a11x1 + a12x2 + … + a1nxn = 0

a21x1 + a22x2 + … + a2nxn = 0

am1x1 + am2x2 + … + amnxn = 0

Setiap sistem persamaan linier yang homogen bersifat adalah tetap apabila semua sistem mepunyaix1 = 0 , x2 = 0 , … , xn = 0 sebagai penyelesaian. Penyelesaian ini disebut solusi trivial. Apabila mempunyai penyelesaian yang lain maka disebut solusi nontrivial.

Penyelesaian Persamaan Linear dengan Matriks

Bentuk Eselon-baris
Operasi Eliminasi Gauss-Jordan

Matriks dapat dikatakan Eselon-baris apabila memenuhi persyaratan berikut :

1.) Di setiap baris, angka pertama selain 0 harus 1 (leading 1).

2.) Jika ada baris yang semua elemennya nol, maka harus dikelompokkan di baris akhir dari matriks.

3.) Jika ada baris yang leading 1 maka leading 1 di bawahnya, angka 1-nya harus berada lebih kanan darileading 1 di atasnya.

4.) Jika kolom yang memiliki leading 1 angka selain 1 adalah nol maka matriks tersebut disebut Eselon-baris tereduksi

Contoh: syarat 1: baris pertama disebut dengan leading 1

$\begin{bmatrix} 1 & 4 & -2 & 5\\ 0 & -5 & 2 & 7\\ 0 & 0 & -3 & 9\\ 0 & 0 & -8 & 8\\ \end{bmatrix}” /></dd> </dl> </dd> </dl> <p style=$ syarat 2: baris ke-3 dan ke-4 memenuhi syarat 2

$\begin{bmatrix} 1 & 4 & -2 & 5\\ 0 & -5 & 2 & 7\\ 0 & 0 & -3 & 9\\ 0 & 0 & 0 & 0\\ \end{bmatrix}” /></dd> </dl> </dd> </dl> <p style=$ syarat 3: baris pertama dan ke-2 memenuhi syarat 3

$\begin{bmatrix} 1 & 4 & -2 & 5\\ 0 & 1 & 2 & 7\\ 0 & 0 & -3 & 9\\ 0 & 0 & 0 & 0\\ \end{bmatrix}” /></dd> </dl> </dd> </dl> <p style=$ syarat 4: matriks dibawah ini memenuhi syarat ke 4 dan disebut Eselon-baris tereduksi

Operasi Eliminasi Gauss

Eliminasi Gauss adalah suatu cara mengoperasikan nilai-nilai di dalam matriks sehingga menjadi matriks yang lebih sederhana (ditemukan oleh Carl Friedrich Gauss). Caranya adalah dengan melakukan operasi baris sehingga matriks tersebut menjadi matriks yang Eselon-baris. Ini dapat digunakan sebagai salah satu metode penyelesaian persamaan linear dengan menggunakan matriks. Caranya dengan mengubah persamaan linear tersebut ke dalam matriks teraugmentasi dan mengoperasikannya. Setelah menjadi matriks Eselon-baris, lakukan substitusi balik untuk mendapatkan nilai dari variabel-variabel tersebut.

Contoh: Diketahui persamaan linear

x + 2y + z = 6

x + 3y + 2z = 9

2x + y + 2z = 12

Tentukan Nilai x, y dan z

Jawab:

Bentuk persamaan tersebut ke dalam matriks:

$\begin{bmatrix} 1 & 2 & 1 & 6\\ 1 & 3 & 2 & 9\\ 2 & 1 & 2 & 12\\ \end{bmatrix}” /></dd> </dl> </dd> </dl> <p style=$ Operasikan Matriks tersebut

$\begin{bmatrix} 1 & 2 & 1 & 6\\ 0 & 1 & 1 & 3\\ 2 & 1 & 2 & 12\\ \end{bmatrix}” /> Baris ke 2 dikurangi baris ke 1 1 & 2 & 1 & 6\\ 0 & 1 & 1 & 3\\ 0 & -3 & 0 & 0\\ \end{bmatrix}” /> Baris ke 3 dikurangi 2 kali baris ke 1 1 & 2 & 1 & 6\\ 0 & 1 & 1 & 3\\ 0 & 0 & 3 & 9\\ \end{bmatrix}” /> Baris ke 3 ditambah 3 kali baris ke 2 1 & 2 & 1 & 6\\ 0 & 1 & 1 & 3\\ 0 & 0 & 1 & 3\\ \end{bmatrix}” /> Baris ke 3 dibagi dengan 3 (Matriks menjadi Eselon-baris) <p style=$ Maka mendapatkan 3 persamaan linier baru yaitu

x + 2y + z = 6

y + z = 3

z = 3

Kemudian lakukan substitusi balik maka didapatkan:

y + z = 3

y + 3 = 3

y = 0

x + 2y + z = 6

x + 0 + 3 = 6

x = 3

Jadi nilai dari x = 3 , y = 0 ,dan z = 3

Eliminasi Gauss-Jordan adalah pengembangan dari eliminasi Gauss yang hasilnya lebih sederhana. Caranya adalah dengan meneruskan operasi baris dari eliminasi Gauss sehingga menghasilkan matriks yang Eselon-baris tereduksi. Ini juga dapat digunakan sebagai salah satu metode penyelesaian persamaan linear dengan menggunakan matriks. Caranya dengan mengubah persamaan linear tersebut ke dalam matriks teraugmentasi dan mengoperasikannya. Setelah menjadi matriks Eselon-baris tereduksi, maka langsung dapat ditentukan nilai dari variabel-variabelnya tanpa substitusi balik.

Contoh: Diketahui persamaan linear

x + 2y + 3z = 3

2x + 3y + 2z = 3

2x + y + 2z = 5

Tentukan Nilai x, y dan z

Jawab:

Bentuk persamaan tersebut ke dalam matriks:

$\begin{bmatrix} 1 & 2 & 3 & 3\\ 2 & 3 & 2 & 3\\ 2 & 1 & 2 & 5\\ \end{bmatrix}” /></dd> </dl> </dd> </dl> <p style=$ Operasikan Matriks tersebut

$\begin{bmatrix} 1 & 2 & 3 & 3\\ 0 & -1 & -4 & -3\\ 2 & 1 & 2 & 5\\ \end{bmatrix}” /> Baris ke 2 dikurangi 2 kali baris ke 1 1 & 2 & 3 & 3\\ 0 & -1 & -4 & -3\\ 0 & -3 & -4 & -1\\ \end{bmatrix}” /> Baris ke 3 dikurangi 2 kali baris ke 1 1 & 2 & 3 & 3\\ 0 & -1 & -4 & -3\\ 0 & 0 & 8 & 8\\ \end{bmatrix}” /> Baris ke 3 dikurangi 3 kali baris ke 2 1 & 2 & 3 & 3\\ 0 & 1 & 4 & 3\\ 0 & 0 & 1 & 1\\ \end{bmatrix}” /> Baris ke 3 dibagi 8 dan baris ke 2 dibagi -1 1 & 2 & 3 & 3\\ 0 & 1 & 0 & -1\\ 0 & 0 & 1 & 1\\ \end{bmatrix}” /> Baris ke 2 dikurangi 4 kali baris ke 3 1 & 2 & 0 & 0\\ 0 & 1 & 0 & -1\\ 0 & 0 & 1 & 1\\ \end{bmatrix}” /> Baris ke 1 dikurangi 3 kali baris ke 3 1 & 0 & 0 & 2\\ 0 & 1 & 0 & -1\\ 0 & 0 & 1 & 1\\ \end{bmatrix}” /> Baris ke 1 dikurangi 2 kali baris ke 2 (Matriks menjadi Eselon-baris tereduksi) <p style=$

Maka didapatkan nilai dari x = 2 , y = − 1 ,dan z = 1

Pages

Contoh dan Penyelesain Matrix

Mengenai Saya

Kamis, 05 Juni 2014

Menyelesaikan Sistem Persamaan Linear dengan Determinan

Menyelesaikan Sistem Persamaan Linear dengan Invers Matriks

Eliminasi Gauss / Eliminasi Gauss-Jordan

Penyelesaian Sistem Persamaan Linear dengan Matriks

Penyelesaian Sistem Persamaan Linear dengan Matriks

Popular Posts

Blogger templates

Blogger news

Blog Archive

Blogroll

About